3.1.6.18. ASDConcrete3D Material

This command is used to construct an ASDConcrete3D material object, a plastic-damage model for concrete and masonry like materials.

It is based on continuum-damage theory, were the stress tensor can be explicitly obtained from the total strain tensor, without internal iterations at the constitutive level. This makes it fast and robust, suitable for the simulation of large-scale structures. Plasticity is added in a simplified way, in order to have the overall effect of inelastic deformation, but keeping the simplicity of continuum-damage models.

To improve robustness and convergence of the simulation in case of strain-softening, this model optionally allows to use the IMPL-EX integration scheme (a mixed IMPLicit EXplicit integration scheme).

nDMaterial ASDConcrete3D $tag $E $v <-rho $rho>

<-fc $fc> <-ft $ft>

<-Te $Te -Ts $Ts <-Td $Td>>

<-Ce $Ce -Cs $Cs <-Cd $Cd>>

<-implex> <-implexControl $implexErrorTolerance $implexTimeReductionLimit> <-implexAlpha $alpha>

<-crackPlanes $nct $ncc $smoothingAngle>

<-eta $eta> <-tangent> <-autoRegularization $lch_ref> <-Kc $Kc>

<-cdf $cdf>

Argument	Type	Description
$tag	integer	Unique tag identifying this material.
$E $v	2 float	Mandatory. Young’s modulus and Poisson’s ratio.
-rho $rho	string + float	Optional. -rho: A keyword that precedes the float. $rho: The mass density.
-fc $fc	string + float	Optional. -fc: A keyword that precedes the float. $fc: The concrete compressive strength.
-ft $ft	string + float	Optional. -ft: A keyword that precedes the float. $ft: The concrete tension (rupture) strength.
-Te $Te	string + list	Optional. -Te: A keyword that precedes the list. $Te: A list of total-strain values for the tensile hardening-softening law. If not specified, $Te will be computed automatically from $fc and $ft. If specified, $Te will override $fc and $ft.
-Ts $Ts	string + list	Optional. -Ts: A keyword that precedes the list. $Ts: A list of stress values for the tensile hardening-softening law. If not specified, $Ts will be computed automatically from $fc and $ft. If specified, $Ts will override $fc and $ft.
-Td $Td	string + list	Optional. -Td: A keyword that precedes the list. $Td: A list of damage values for the tensile hardening-softening law. If not defined, no stiffness degradation will be considered. If not specified, $Td will be computed automatically from $fc and $ft. If specified, $Td will override $fc and $ft.
-Ce $Ce	string + list	Optional. -Ce: A keyword that precedes the list. $Ce: A list of total-strain values for the compressive hardening-softening law. If not specified, $Ce will be computed automatically from $fc and $ft. If specified, $Ce will override $fc and $ft.
-Cs $Cs	string + list	Optional. -Cs: A keyword that precedes the list. $Cs: A list of stress values for the compressive hardening-softening law. If not specified, $Cs will be computed automatically from $fc and $ft. If specified, $Cs will override $fc and $ft.
-Cd $Cd	string + list	Optional. -Cd: A keyword that precedes the list. $Cd: A list of damage values for the compressive hardening-softening law. If not defined, no stiffness degradation will be considered. If not specified, $Cd will be computed automatically from $fc and $ft. If specified, $Cd will override $fc and $ft.
-implex	string	Optional. If defined, the IMPL-EX integration will be used, otherwise the standard implicit integration will be used (default).
-implexControl $implexErrorTolerance $implexTimeReductionLimit	string + 2 float	Optional. -implexControl: Activates the control of the IMPL-EX error. implexErrorTolerance: Relative error tolerance. implexTimeReductionLimit: Minimum allowed relative reduction of the time-step. If the error introduced by the IMPL-EX algorithm is larger than implexErrorTolerance , the material will fail during the computation. The user can therfore use an adaptive time-step to reduce the time-step to keep the error under control. If the reduction of the time-step is smaller than implexTimeReductionLimit , the error control will be skipped. Suggested values: -implexControl 0.05 0.01.
-implexAlpha $alpha	string + float	Optional. Default = 1. The \(\alpha\) coefficient for the explicit extrapolation of the internal variables in the IMPL-EX algorithm. It can range from 0 to 1.
-crackPlanes $nct $ncc $smoothingAngle	string + 2 integer + float	Optional. If defined, it activates the anisotropy of internal variables. Tensile internal variables are stored on crack-planes that are equally spaced every \(90/nc_t\) degrees. Compressive internal variables are stored on crack-planes that are equally spaced every \(90/nc_c\) degrees. The active crack-plane is chosen based on the current principal stress directions. smoothingAngle: Angle in degrees used to smooth the internal variables on crack-planes around the active crack-plane. Suggested values: -crackPlanes 4 4 45.0
-eta $eta	string + float	Optional. If defined, the rate-dependent model is used (By default the model is rate-independent). -eta: Activates the rate-dependent model. eta: The viscosity parameter \(\eta\), representing the relaxation time of the viscoplastic system.
-tangent	string	Optional. If defined, the tangent constitutive matrix is used. By default, the secant stiffness is used.
-autoRegularization $lch_ref	string + float	Optional. If defined, and if the tensile and/or the compressive hardening-softening law has strain-softening, the area under the hardening-softening law is assumed to be a real fracture energy (\(G_f\) with dimension = \(F/L\)), and the specific fracture energy \(g_f\) (with dimension = \(F/L^2\)) is automatically computed as \(g_f=G_f/l_{ch}\), where \(l_{ch}\) is the characteristic length of the Finite Element. In this case $lch_ref is 1. If, instead, the area is a specific fracture energy (\(g_{f,ref}\) with dimension = \(F/L^2\)), $lch_ref should be set equal to the experimental size used to obtain the strain from the displacement jump. In this case, the regularization will be performed as \(g_f=G_f/l_{ch} = g_{f,ref}*l_{ch,ref}/l_{ch}\)
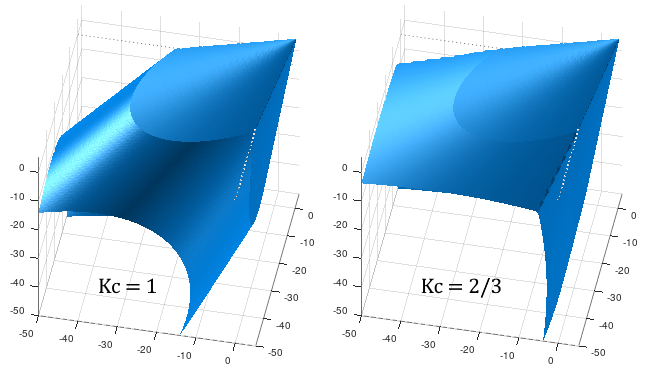
-Kc $Kc	string + float	Optional. -Kc: A keyword that precedes the float. $Kc: A coefficient that defines the shape of the failure surface in triaxial compression. It must be \(1/2 < K_c <= 1\), default = \(2/3\). The lower \(K_c\), the stronger is the material in triaxial compression: Fig. 3.1.6.2 Effect of \(K_c\) on the triaxial-compression part of the failure surface.
-cdf $cdf	string + float	Optional (default = 0). The Cross-Damage-Factor (cdf) control the dilatancy of the material. cdf should be >= 0. The larger cdf, the smaller the dilatancy. 0 is the optimal value for concrete.

3.1.6.18.1. Theory

In the following description, all variables without subscripts refer to the current time-step, while those with the \(n\) and \(n-1\) subscripts refer to the same variables at the two previous (known) time steps.

The trial effective stress tensor is computed from the previous effective stress \(\bar{\sigma}_{n}\) and the trial elastic stress increment \(C_{0}:\left (\varepsilon - \varepsilon_{n}\right )\):

\[\tilde{\sigma} = \bar{\sigma}_{n} + C_{0}:\left (\varepsilon - \varepsilon_{n}\right )\]

It is then split into its positive (\(\tilde{\sigma}^{+}\)) and negative (\(\tilde{\sigma}^{-}\)) parts, using the positive principal stresses (\(\langle \tilde{\sigma}_{i} \rangle\)) and their principal directions (\(p_{i}\)):

\[\begin{align} \tilde{\sigma}^{+} = \sum_{i=1}^{3} \langle \tilde{\sigma}_{i} \rangle p_{i}\otimes p_{i} && \tilde{\sigma}^{-} = \tilde{\sigma} - \tilde{\sigma}^{+} \end{align}\]

Two equivalent scalar stress measures for the tensile (\(\tilde{\tau}^+\)) and compressive (\(\tilde{\tau}^-\)) behaviors are obtained from the trial effective stress tensor \(\tilde{\sigma}\) (or from its negative part \(\tilde{\sigma}^{-}\) for the compressive behavior) using the following damage surfaces:

\[\tilde{\tau}^+ = f\left(\tilde{\sigma} \right) = H\left (\tilde{\sigma}_{max} \right )\left [\frac{1}{1-\alpha}\left(\alpha\tilde{I}_1+\sqrt[]{3\tilde{J}_2}+\beta\langle \tilde{\sigma}_{max} \rangle \right )\frac{1}{\phi} \right ]\]

\[\tilde{\tau}^- = f\left(\tilde{\sigma}^{-} \right) = \left [\frac{1}{1-\alpha}\left(\alpha\tilde{I}_1+\sqrt[]{3\tilde{J}_2}+\gamma\langle -\tilde{\sigma}_{max} \rangle \right ) \right ]\]

where \(\tilde{I}_1\) is the first invariant of \(\tilde{\sigma}\) (or \(\tilde{\sigma}^{-}\)), \(\tilde{J}_2\) is the second invariant of the deviator of \(\tilde{\sigma}\) (or \(\tilde{\sigma}^{-}\)), \(\sigma_{max}\) is the maximum principal stress of \(\tilde{\sigma}\) (or \(\tilde{\sigma}^{-}\)), \(\alpha = 4/33\), \(\beta = 23/3\), \(\phi = 10\), \(\gamma= 3(1 - K_c) / (2 K_c - 1)\).

The equivalent stress measures \(\tilde{\tau}^+\) and \(\tilde{\tau}^-\) are converted into their trial total-strain counter-parts \(\tilde{x}^+\) and \(\tilde{x}^-\) accounting for the equivalent plastic strain from the previous step:

\[\tilde{x}^{\pm} = \frac{\tilde{\tau}^{\pm}}{E} + x_{pl,n}\]

To impose the irreversibity of plasticity and damage, and to account for rate-dependency (if \(\eta \gt 0\)), the current equivalent strain measures are updated as follows:

\[\begin{split}x^{\pm} = \begin{cases} \frac{\eta}{\eta +\Delta t} x^{\pm}_n + \frac{\Delta t}{\eta +\Delta t} \tilde{x}^{\pm}, & \text{if } \tilde{x}^{\pm} > x^{\pm}_n\\ x^{\pm}_n, & \text{otherwise} \end{cases}\end{split}\]

The equivalent total-strain measures are then plugged into the hardening-softening laws to obtain the plastic and cracking damage variables \(d_{pl}^{\pm}\) and \(d_{cr}^{\pm}\), and the effective (\(\bar{\sigma}\)) and nominal (\(\sigma\)) stress tensors are computed as:

\[\begin{align} \bar{\sigma}^+ = \left (1-d^{+}_{pl}\right ) \tilde{\sigma}^+, && \bar{\sigma}^- = \left (1-d^{-}_{pl}\right ) \tilde{\sigma}^-, && \bar{\sigma} = \bar{\sigma}^+ + \bar{\sigma}^- \end{align}\]

\[\sigma = \left (1-d^{+}_{cr}\right ) \bar{\sigma}^+ + \left (1-d^{-}_{cr}\right ) \bar{\sigma}^-\]

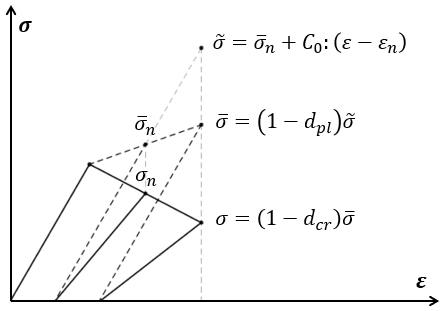
Fig. 3.1.6.3 A schematic representation of the elastic predictor followed by the plastic and damage correctors in a representative uniaxial case.

3.1.6.18.2. Usage Notes

Responses

• All responses available for the nDMaterial object: stress (or stresses), strain (or strains), tangent (or Tangent), TempAndElong.

• damage or Damage: 2 components (\(d^+\), \(d^-\)). The cracking damage variables. If option -crackPlanes is used, it gives the maximum values among all crack-planes.

• damage -avg or Damage -avg: 2 components (\(d^+\), \(d^-\)). Same as above. If option -crackPlanes is used, it gives the average values of the crack-planes.

• equivalentPlasticStrain or EquivalentPlasticStrain: 2 components (\(x_{pl}^+\), \(x_{pl}^-\)). The equivalent plastic strains. If option -crackPlanes is used, it gives the maximum values among all crack-planes.

• equivalentPlasticStrain -avg or EquivalentPlasticStrain -avg: 2 components (\(x_{pl}^+\), \(x_{pl}^-\)). Same as above. If option -crackPlanes is used, it gives the average values of the crack-planes.

• equivalentTotalStrain or EquivalentTotalStrain: 2 components (\(x^+\), \(x^-\)). The equivalent total strains. If option -crackPlanes is used, it gives the maximum values among all crack-planes.

• equivalentTotalStrain -avg or EquivalentTotalStrain -avg: 2 components (\(x^+\), \(x^-\)). Same as above. If option -crackPlanes is used, it gives the average values of the crack-planes.

• cw or crackWidth or CrackWidth: 1 component (\(cw\)). The equivalent tensile total strain minus the equivalent strain at the onset of crack, times the characteristic length of the parent element. If option -crackPlanes is used, it gives the maximum value among all crack-planes.

• cw -avg or crackWidth -avg or CrackWidth -avg: 1 component (\(cw\)). Same as above. If option -crackPlanes is used, it gives the average value of the crack-planes.

• crackInfo $Nx $Ny $Nz or CrackInfo $Nx $Ny $Nz: 2 components (\(ID\), \(X\)). Gives the 0-based index (ID) and the tensile equivalent total strain (X) of the crack-plane with the normal vector closest to (Nx, Ny, Nz).

• crushInfo $Nx $Ny $Nz or CrushInfo $Nx $Ny $Nz: 2 components (\(ID\), \(X\)). Same as above, but for the compressive response.

Example 1 - Drawing the Damage Surface

A Python example to draw the damage surface in the plane-stress case: ASDConcrete3D_Ex_Surface.py

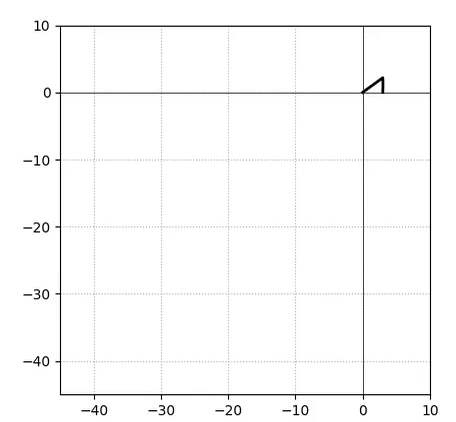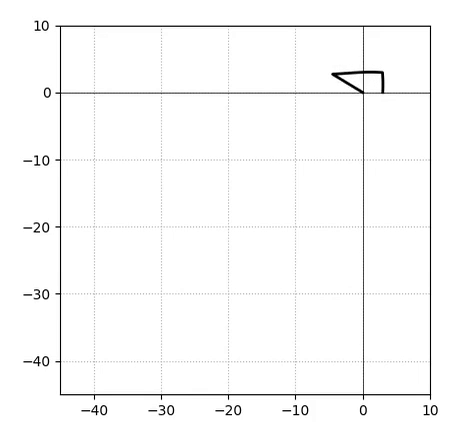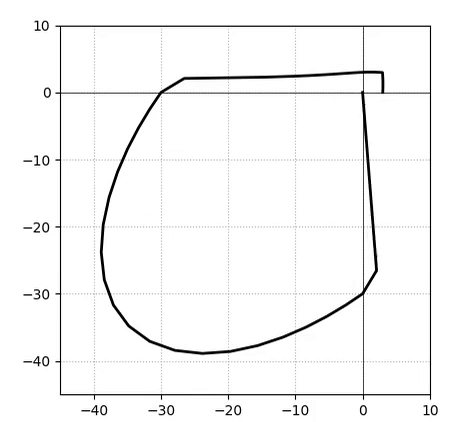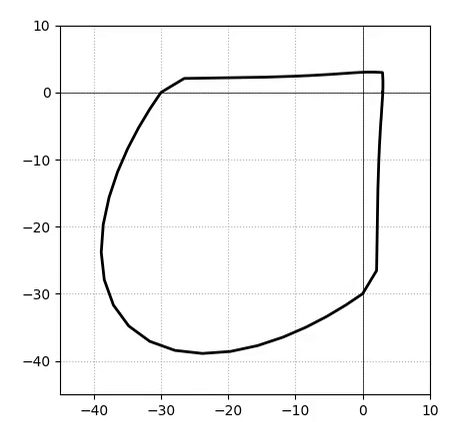
Example 2 - Understanding the Hardening/Softening Laws

A Python module to generate typical hardening-softening laws for normal concrete: ASDConcrete3D_MakeLaws.py

Simple example to test it under uniaxial conditions in tension and compression: ASDConcrete3D_Ex_CyclicUniaxialTension.py and ASDConcrete3D_Ex_CyclicUniaxialCompression.py

3.1.6.18.3. References

[Petracca2022]

Petracca, M., Camata, G., Spacone, E., & Pelà, L. (2022). “Efficient Constitutive Model for Continuous Micro-Modeling of Masonry Structures” International Journal of Architectural Heritage, 1-13 (Link to article)

[Oliver2008]

Oliver, J., Huespe, A. E., & Cante, J. C. (2008). “An implicit/explicit integration scheme to increase computability of non-linear material and contact/friction problems” Computer Methods in Applied Mechanics and Engineering, 197(21-24), 1865-1889 (Link to article)

Code Developed by: Massimo Petracca at ASDEA Software, Italy.