3.1.6.14. Orthotropic Material Wrapper

This command is used to construct an Orthotropic material object. It is a wrapper that can convert any 3D (Linear or Nonlinear) constitutive model to an orthotropic one.

nDMaterial Orthotropic $matTag $theIsoMatTag $Ex $Ey $Ez $Gxy $Gyz $Gzx $vxy $vyz $vzx $Asigmaxx $Asigmayy $Asigmazz $Asigmaxyxy $Asigmayzyz $Asigmaxzxz

Argument	Type	Description
$matTag	integer	unique tag identifying this orthotropic material wrapper
$theIsoMatTag	integer	unique tag identifying a previously defined isotropic material
$Ex $Ey $Ez	3 float	Elastic moduli in three mutually perpendicular directions
$Gxy $Gyz $Gzx	3 float	Shear moduli
$vxy $vyz $vzx	3 float	Poisson’s ratios
$Asigmaxx	float	Ratio of the isotropic to the orthotropic strength along the X direction (Fxx_iso / Fxx_ortho)
$Asigmayy	float	Ratio of the isotropic to the orthotropic strength along the Y direction (Fyy_iso / Fyy_ortho)
$Asigmazz	float	Ratio of the isotropic to the orthotropic strength along the Z direction (Fzz_iso / Fzz_ortho)
$Asigmaxyxy	float	Ratio of the isotropic to the orthotropic shear strength in the XY plane (Fxy_iso / Fxy_ortho)
$Asigmayzyz	float	Ratio of the isotropic to the orthotropic shear strength in the YZ plane (Fyz_iso / Fyz_ortho)
$Asigmaxzxz	float	Ratio of the isotropic to the orthotropic shear strength in the XZ plane (Fxz_iso / Fxz_ortho)

3.1.6.14.1. Usage Notes

Note 1

The only material formulation for the Orthotropic material object is “ThreeDimensional”.

Note 2

The only material formulation allowed for the adapted isotropic material object is “ThreeDimensional”.

Example

A simple example which evaluates the Yield domain in the plane-stress plane (Szz = 0) of the original isotropic J2Plasticity model (Sy = 400 MPa) and of its orthotropic counter-part (Sx = 1.5*Sy, Ex = 1.5*Ey).
The Tcl code prints the points of the two yield domains on the screen.
The Python code creates a plot like this:

../../../../_images/Orthotropic_result.png

Python Code

from openseespy import opensees as os
import math
from matplotlib import pyplot as plt

def analyze_dir (dX, dY, type):

    # info
    print("Analyze direction (%g, %g)" % (dX, dY))

    # the 2D model
    os.wipe()
    os.model( "basic", "-ndm", 2, "-ndf", 2 )

    # the material
    E = 200000.0
    v = 0.3
    G = E/(2.0*(1.0+v))
    K = E/(3.0*(1.0-2.0*v))
    sig0 = 400.0
    os.nDMaterial( "J2Plasticity", 1, K, G, sig0, sig0, 0.0, 0.0 )

    # the orthotropic wrapper
    if type == "ortho":
        Ex = E*1.5
        Ey = E
        Ez = E
        Gxy = G
        Gyz = G
        Gzx = G
        vxy = v
        vyz = v
        vzx = v
        Asigmaxx = 1.0/1.5 # fx_iso/fx_ortho
        # nDMaterial Orthotropic $tag $theIsoMat $Ex $Ey $Ez $Gxy $Gyz $Gzx $vxy $vyz $vzx $Asigmaxx $Asigmayy $Asigmazz $Asigmaxyxy $Asigmayzyz $Asigmaxzxz.
        os.nDMaterial( "Orthotropic", 2, 1, Ex, Ey, Ez, Gxy, Gyz, Gzx, vxy, vyz, vzx, Asigmaxx, 1.0, 1.0, 1.0, 1.0, 1.0)
        os.nDMaterial( "PlaneStress", 3, 2)

    # a triangle
    os.node( 1, 0, 0 )
    os.node( 2, 1, 0 )
    os.node( 3, 0, 1 )
    os.element( "tri31", 1,   1, 2, 3,   1.0, "PlaneStress", 3 if type == "ortho" else 1 )

    # fixity
    os.fix( 1,   1, 1)
    os.fix( 2,   0, 1)
    os.fix( 3,   1, 0)

    # a simple ramp
    os.timeSeries( "Linear", 1, "-factor", 2.0*sig0 )

    # imposed stresses
    os.pattern( "Plain", 1, 1 )
    os.load( 2, dX, 0.0 )
    os.load( 3, 0.0, dY )

    # analyze
    os.constraints( "Transformation" )
    os.numberer( "Plain" )
    os.system( "FullGeneral" )
    os.test( "NormDispIncr", 1.0e-6, 3, 0)
    os.algorithm( "Newton" )

    dLambda = 0.1
    dLambdaMin = 0.001
    Lambda = 0.0
    sX = 0.0
    sY = 0.0
    while 1 :
        os.integrator( "LoadControl", dLambda )
        os.analysis( "Static" )
        ok = os.analyze( 1 )
        if ok == 0:
            stress = os.eleResponse( 1, "material", 1, "stress" )
            sX = stress[0]
            sY = stress[1]
            Lambda += dLambda
            if Lambda > 0.9999:
                break
        else:
            dLambda /= 2.0
            if dLambda < dLambdaMin:
                break

    # done
    return (sX, sY)

NDiv = 48
NP = NDiv+1
dAngle = 2.0*math.pi/NDiv
SX = [0.0]*NP
SY = [0.0]*NP
SXortho = [0.0]*NP
SYortho = [0.0]*NP
for i in range(NDiv):
    angle = i*dAngle
    dX = math.cos(angle)
    dY = math.sin(angle)
    iso = analyze_dir(dX, dY, "iso")
    ortho = analyze_dir(dX, dY, "ortho")
    SX[i] = iso[0]
    SY[i] = iso[1]
    SXortho[i] = ortho[0]
    SYortho[i] = ortho[1]
SX[-1] = SX[0]
SY[-1] = SY[0]
SXortho[-1] = SXortho[0]
SYortho[-1] = SYortho[0]

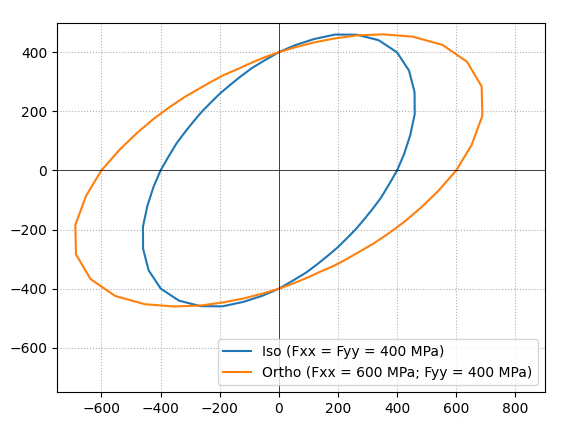
fig, ax = plt.subplots(1,1)
ax.plot(SX, SY, label='Iso (Fxx = Fyy = 400 MPa)')
ax.plot(SXortho, SYortho, label='Ortho (Fxx = 600 MPa; Fyy = 400 MPa)')
ax.grid(linestyle=':')
ax.set_aspect('equal', 'box')
ax.set(xlim=[-750, 900],ylim=[-750, 500])
ax.plot([-1000,1000],[0,0],color='black',linewidth=0.5)
ax.plot([0,0],[-1000,1000],color='black',linewidth=0.5)
ax.legend(loc='lower right')
plt.show()

Tcl Code

proc analyze_dir {dX dY type} {

    # info
    puts "Analyze direction ($dX, $dY)"

    # the 2D model
    wipe
    model basic -ndm 2 -ndf 2

    # the isotropic material
    set E 200000.0
    set v 0.3
    set G [expr $E/(2.0*(1.0+$v))]
    set K [expr $E/(3.0*(1.0-2.0*$v))]
    set sig0 400.0
    nDMaterial J2Plasticity 1 $K $G $sig0 $sig0 0.0 0.0

    # the orthotropic wrapper
    if {$type == "ortho"} {
        set Ex [expr $E*1.5]
        set Ey $E
        set Ez $E
        set Gxy $G
        set Gyz $G
        set Gzx $G
        set vxy $v
        set vyz $v
        set vzx $v
        set Asigmaxx [expr 1.0/1.5]; # fx_iso/fx_ortho
        # nDMaterial Orthotropic $tag $theIsoMat $Ex $Ey $Ez $Gxy $Gyz $Gzx $vxy $vyz $vzx $Asigmaxx $Asigmayy $Asigmazz $Asigmaxyxy $Asigmayzyz $Asigmaxzxz.
        nDMaterial Orthotropic 2 1 $Ex $Ey $Ez $Gxy $Gyz $Gzx $vxy $vyz $vzx $Asigmaxx 1.0 1.0 1.0 1.0 1.0
        nDMaterial PlaneStress 3 2
    }

    # a triangle
    node 1 0 0
    node 2 1 0
    node 3 0 1
    if {$type == "ortho"} {
        set mat_tag 3
    } else {
        set mat_tag 1
    }
    element tri31 1   1 2 3   1.0 "PlaneStress" $mat_tag

    # fixity
    fix 1   1 1
    fix 2   0 1
    fix 3   1 0

    # a simple ramp
    timeSeries Linear 1 -factor [expr 2.0*$sig0]

    # imposed stresses
    pattern Plain 1 1 {
        load 2 $dX 0.0
        load 3 0.0 $dY
    }

    # analyze
    constraints Transformation
    numberer Plain
    system FullGeneral
    test NormDispIncr 1.0e-6 3 0
    algorithm Newton

    set dLambda 0.1
    set dLambdaMin 0.001
    set Lambda 0.0
    set sX 0.0
    set sY 0.0
    while 1 {
        integrator LoadControl $dLambda
        analysis Static
        set ok [analyze 1]
        if {$ok == 0} {
            set stress [eleResponse 1 "material" 1 "stress"]
            set sX [expr [lindex $stress 0]]
            set sY [expr [lindex $stress 1]]
            set Lambda [expr $Lambda + $dLambda]
            if {$Lambda > 0.9999} {
                break
            }
        } else {
            set dLambda [expr $dLambda/2.0]
            if {$dLambda < $dLambdaMin} {
                break
            }
        }
    }

    # done
    return [list $sX $sY]
}

set NDiv 48
set NP [expr $NDiv+1]
set pi [expr acos(-1)]
set dAngle [expr 2.0*$pi/$NDiv]
set SX {}
set SY {}
set SXortho {}
set SYortho {}
for {set i 0} {$i < $NDiv} {incr i} {
    set angle [expr $i.0*$dAngle]
    set dX [expr cos($angle)]
    set dY [expr sin($angle)]
    set iso [analyze_dir $dX $dY "iso"]
    set ortho [analyze_dir $dX $dY "ortho"]
    lappend SX [lindex $iso 0]
    lappend SY [lindex $iso 1]
    lappend SXortho [lindex $ortho 0]
    lappend SYortho [lindex $ortho 1]
}
lappend SX [lindex $SX 0]
lappend SY [lindex $SY 0]
lappend SXortho [lindex $SXortho 0]
lappend SYortho [lindex $SYortho 0]
puts [format "%12s %12s %12s %12s" "Sx(iso)" "Sy(iso)" "Sx(ortho)" "Sy(ortho)"]
for {set i 0} {$i < $NP} {incr i} {
    puts [format "%12.3f %12.3f %12.3f %12.3f" [lindex $SX $i] [lindex $SY $i] [lindex $SXortho $i] [lindex $SYortho $i]]
}

[Oller2003]

Oller, S., Car, E., & Lubliner, J. (2003). Definition of a general implicit orthotropic yield criterion. Computer methods in applied mechanics and engineering, 192(7-8), 895-912. (Link to article)

Code Developed by: Massimo Petracca at ASDEA Software, Italy.