3.1.5.22. BoucWenInfill Material

This command is used to construct the uniaxial BoucWenInfill material producing smooth hysteretic loops with stiffness and strength degradation and pinching effect. The pinching formulation is particularly suitable to simulate the behavior of infill panels and masonry walls.

uniaxialMaterial BoucWenInfill $matTag $mass $alpha $beta0 $eta0 $n $k $xy $deltak $deltaf $psi $Zs $As $epsp $tol $maxIter

Argument	Type	Description
$matTag	integer	integer tag identifying material.
$mass	float	mass of the system.
$alpha	float	ratio of post-yield stiffness to the initial elastic stiffness (0<$alpha<1).
$beta0 $eta0	float	parameters that control the shape of the hysteresis loop (-1<$eta0<1).
$n	float	Parameter that controls the transition from linear to nonlinear range.
$k	float	Initial elastic stiffness.
$xy	float	yielding displacement of the system
$deltak $deltaf	float	Parameters that control respectively stiffness and strength degradation.
$psi	float	Parameter that controls the rate of stiffness degradation.
$Zs	float	parameter that controls the extension of pinching along z-axis.
$As	float	parameter that controls the extension of pinching along x-axis.
$epsp	float	pinching activation energy.
$tol	float	tolerance in each integration step.
$maxIter	float	maximum number of iterations for each integration step.

Note

The determination of constitutive parameters is supported by their physical meaning. In case of infill panels, empirical correlation laws between the model parameters and the geometrical and mechanical properties of infilled frames can be found in [SirottiEtAL2021].

The equations governing the BoucWenInfill behavior are described in [SirottiEtAl2021]. Other references can be found in [PelliciariEtAl2020] for stiffness and strength degradation and in [MadanEtAl1997] for the pinching formulation.

The model may reproduce either force-displacement or stress-strain relationships.

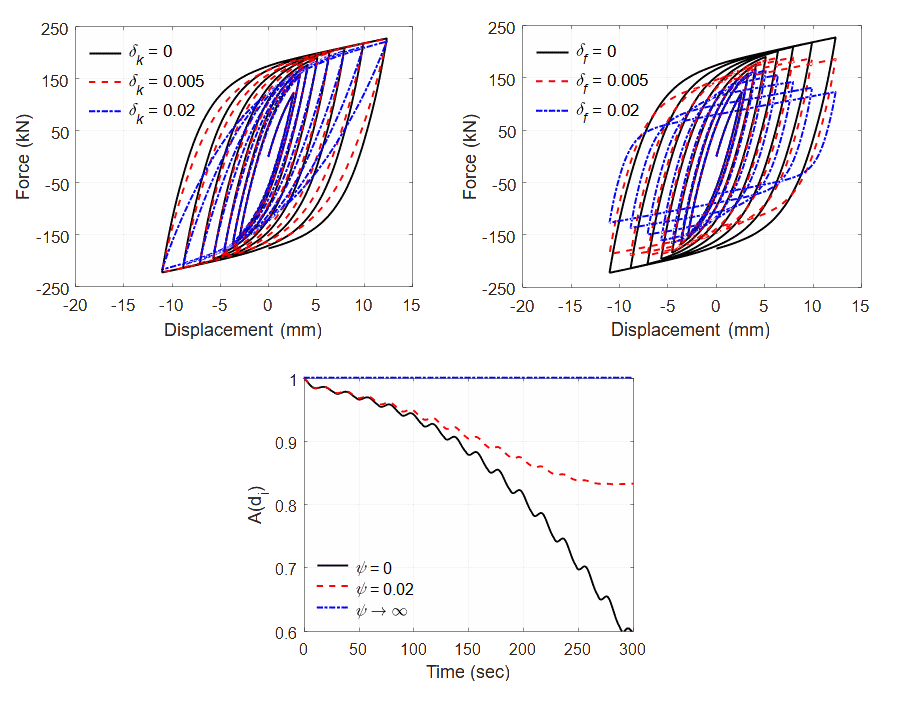
Parameters $deltak, $deltaf and $psi regulate respectively stiffness, strength degradation and the rate of stiffness degradation.

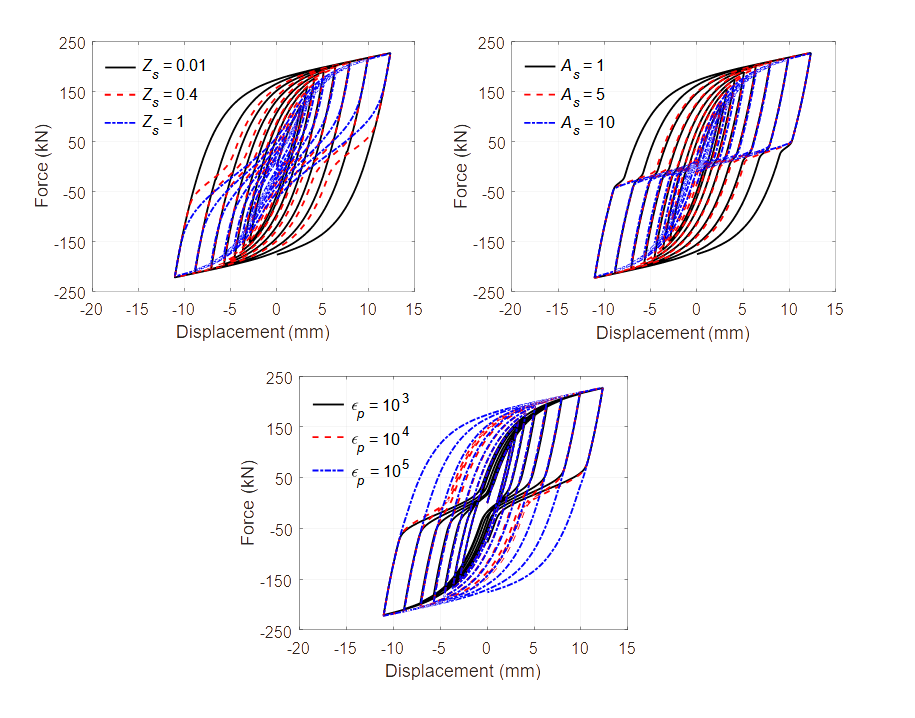
Parameters $Zs, $As and $epsp control the amount and activation of the pinching effect:

Example

The following instruction builds a BoucWenInfill material with tag 1, parameters reported in the table above, tolerance $tol = \(10^{-6}\) and maximum number of iterations $maxIter = \(10^{6}\).

Tcl Code

uniaxialMaterial BoucWenInfill 1 1 0.06 0.25 0.1 1.2 65 1 0.005 0.005 0.001 0.01 5 10000 10e-6 10e6

Code Developed by: Stefano Sirotti, University of Modena and Reggio Emilia, Italy, stefano.sirotti@unimore.it

[SirottiEtAL2021] (1,2)

Sirotti, S., Pelliciari, M., Di Trapani, F., Briseghella, B., Carlo Marano, G., Nuti, C., & Tarantino, A. M. (2021). Development and validation of new Bouc–Wen data-driven hysteresis model for masonry infilled RC frames. Journal of Engineering Mechanics, 147(11), 04021092. DOI: https://doi.org/10.1061/(ASCE)EM.1943-7889.0002001.

[PelliciariEtAl2020]

Pelliciari, M., Briseghella, B., Tondolo, F., Veneziano, L., Nuti, C., Greco, R., … & Tarantino, A. M. (2020). A degrading Bouc–Wen model for the hysteresis of reinforced concrete structural elements. Structure and Infrastructure Engineering, 16(7), 917-930. DOI: https://doi.org/10.1080/15732479.2019.1674893.

[MadanEtAl1997]

Madan, A., Reinhorn, A. M., Mander, J. B., & Valles, R. E. (1997). Modeling of masonry infill panels for structural analysis. Journal of structural engineering, 123(10), 1295-1302. DOI: https://doi.org/10.1061/(ASCE)0733-9445(1997)123:10(1295).