3.1.5.23. HystereticPoly Material

This command is used to construct the uniaxial HystereticPoly material producing smooth hysteretic loops and local maxima/minima. It is based on a polynomial formulation of its tangent stiffness.

uniaxialMaterial HystereticPoly $matTag $ka $kb $alpha $beta1 $beta2 <$delta>

Argument	Type	Description
$matTag	integer	integer tag identifying material.
$ka	float	Tangent stiffness of the initial “elastic” part of the loop.
$kb	float	Tangent stiffness of the asymptotic part of the loop.
$alpha	float	Parameter governing the amplitude of the loop.
$beta1	float	Parameter governing the shape of the asymptotic region of the loop.
$beta2	float	Parameter governing the shape of the asymptotic region of the loop.
$delta	float	Asymptotic tolerance (optional. Default 1.0e-20).

Note

Determination of constitutive parameters is quite intuitive and is reported below, although, their identification can be performed by the strategy formulated in [SessaEtAl2020] implemented in the freeware available here.

The original formulation of HystereticPoly is reported in [VaianaEtAl2019]. Minor changes have been made in its implementation for OpenSees and make reference to the enhanced formulation reported in [SessaEtAl2022] and [Sessa2022].

The model may reproduce either force-displacement or stress-strain relationships. It is formulated by means of two asymptotic lines (blue) linked by transition curves (red):

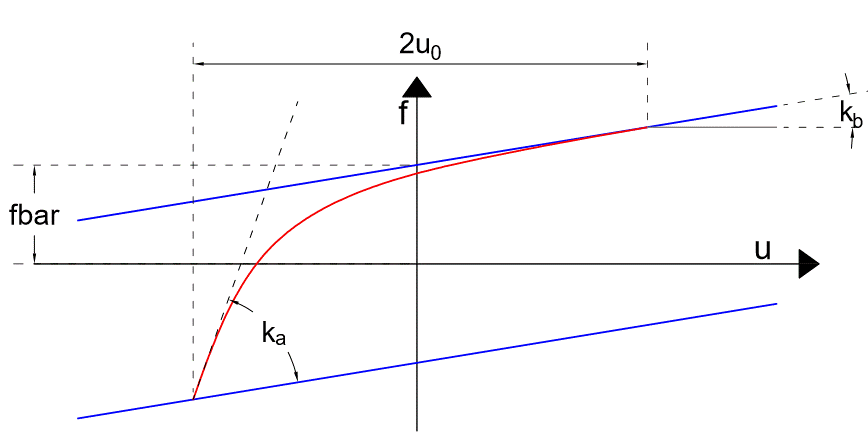
Parameter $alpha governs the transition between such curves so that:

\(u_0=\frac{1}{2}\left[\left(\frac{k_a-k_b}{\delta}\right)^{1/\alpha}-1\right]\)

\(\bar{f}=\frac{k_a-k_b}{2}\left[\frac{\left(1+2u_0\right)^{1-\alpha}-1}{1-\alpha}\right]\)

Where \(\bar{f}\) is the value at which the asymptotic line crosses the vertical axis and \(2u_0\) is the generalized displacement for which the transition curve reaches the asymptotic line.

In general, $alpha= \(\alpha\) influences the amplitude of the loop:

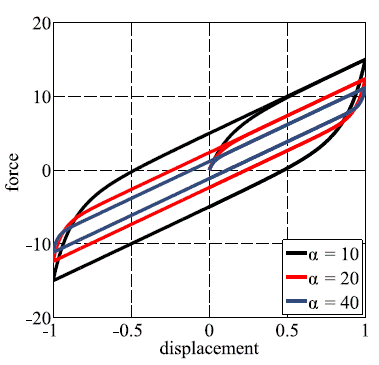
while parameters $beta1 and $beta2 modify the shape of the loop:

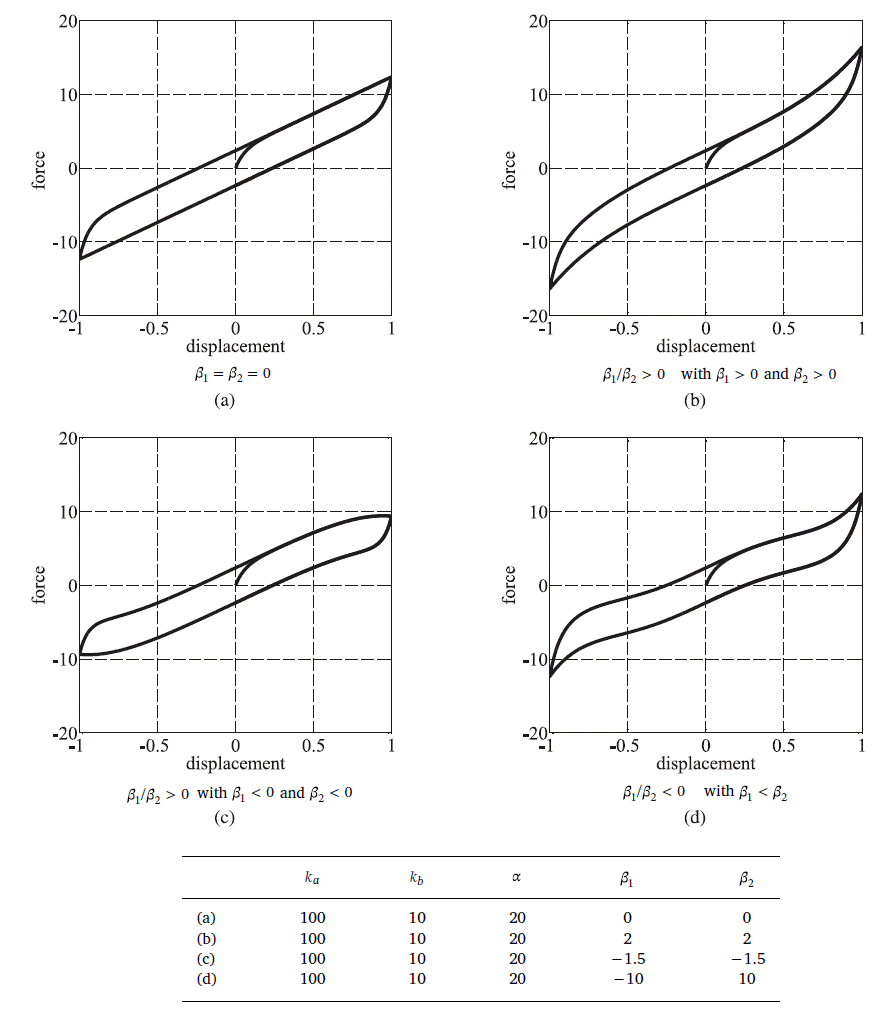
Example

The following constructs a HystereticPoly material with tag 1, parameters corresponding to line (d) of the table above and tolerance $delta = \(10^{-20}\).

1. Tcl Code

uniaxialMaterial HystereticPoly 1  100.0 10.0 20.0 -10.0 10.0 1.0e-20

2. Python Code

uniaxialMaterial('HystereticPoly', 1, 100.0, 10.0, 20.0, -10.0, 10.0, 1.0e-20)

Code Developed by: Salvatore Sessa, University of Naples Federico II, Italy

[VaianaEtAl2019]

Vaiana, N., Sessa, S., Marmo, F. and Rosati, L. (2019). “An accurate and computationally efficient uniaxial phenomenological model for steel and fiber reinforced elastomeric bearings.” Composite Structures, 211: 196-212. DOI: https://doi.org/10.1016/j.compstruct.2018.12.017

[SessaEtAl2020]

Sessa, S., Vaiana, N., Paradiso, M. and Rosati, L. (2020). “An inverse identification strategy for the mechanical parameters of a phenomenological hysteretic constitutive model.”, Mechanical Systems and Signal Processing, 139: 106622. DOI: https://doi.org/10.1016/j.ymssp.2020.106622

[SessaEtAl2022]

Sessa, S., Vaiana, N., Paradiso, M. and Rosati, L. (2022). “Thermodynamic Compatibility of the HystereticPoly Uniaxial Material Implemented in OpenSees.”, Advanced Structured Materials, 175: 565 - 580. DOI: https://doi.org/10.1007/978-3-031-04548-6_27

[Sessa2022]

Sessa, S. (2022). “Thermodynamic compatibility conditions of a new class of hysteretic materials.”, Continuum Mechanics and Thermodynamics, 34(1): 61 - 79. DOI: https://doi.org/10.1007/s00161-021-01044-w