3.1.5.24. HystereticAsym Material (Smooth asymmetric hysteresis)

This command is used to construct the uniaxial HystereticAsym material proposed by Vaiana et al. [VaianaEtAl2021]. It produces smooth and asymmetric hysteretic loops with hardening-softening behavior.

uniaxialMaterial HystereticAsym $matTag $ka $kb $fo $beta1 $beta2 $gamma  <-alpha>

Argument	Type	Description
$matTag	integer	integer tag identifying material.
$ka	float	Tangent stiffness of the initial “elastic” part of the loop.
$kb	float	Tangent stiffness at zero displacement/strain.
$f0	float	Hysteresys force/stress at zero displacement/strain.
$beta1	float	Parameter governing hardening/softening behavior and asymmetry.
$beta2	float	Parameter governing hardening/softening behavior and asymmetry.
$gamma	float	Parameter governing hardening/softening behavior and asymmetry.
-alpha	string	Optional flag: if activated the 3rd parameter is “alpha” instead of “f0” (see below for the details).

Note

The HystereticAsym material provides the response sensitivity for reliability and parametric analysis. Possible calls for the parameters are ‘ka’, ‘kb’, ‘fo’, ‘b1’, ‘b2’ and ‘gamma’.

The equations describing HystereticAsym behavior are described in [VaianaEtAl2021]. Only minor changes have been made in its implementation for OpenSees. The model may reproduce either force-displacement or stress-strain relationships.

The model works as a sort of smooth, bilinear model whose response is modulated by nonlinear functions in order to obtain hardening, softening and asymmetry. Specifically, if \(\beta_1 = \beta_2 = \gamma = 0\) then the loop is symmetric and bilinear:

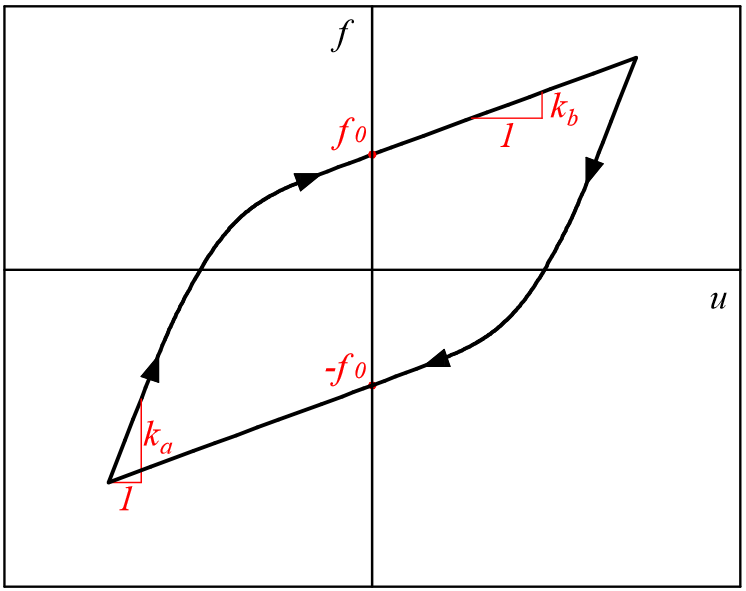
parameter $ka is the initial stiffness of each branch (at the load inversion) while $kb is the hysteresys force/strain at zero displacement. Yielding is ruled by a parameter \(\alpha\) determining the transition between the initial \(k_a\) and final \(k_b\) stiffness. This parameter is also related to the loop amplitude by means of:

\(f_0=\frac{k_a-k_b}{2\alpha}\)

that is represented in figure. Because of the biunivocal relationship between \(f_0\) and \(\alpha\), both can be used as input parameters. The default syntax uses \(f_0\) although it is possible to provide \(\alpha\) by adding the flag “-alpha”.

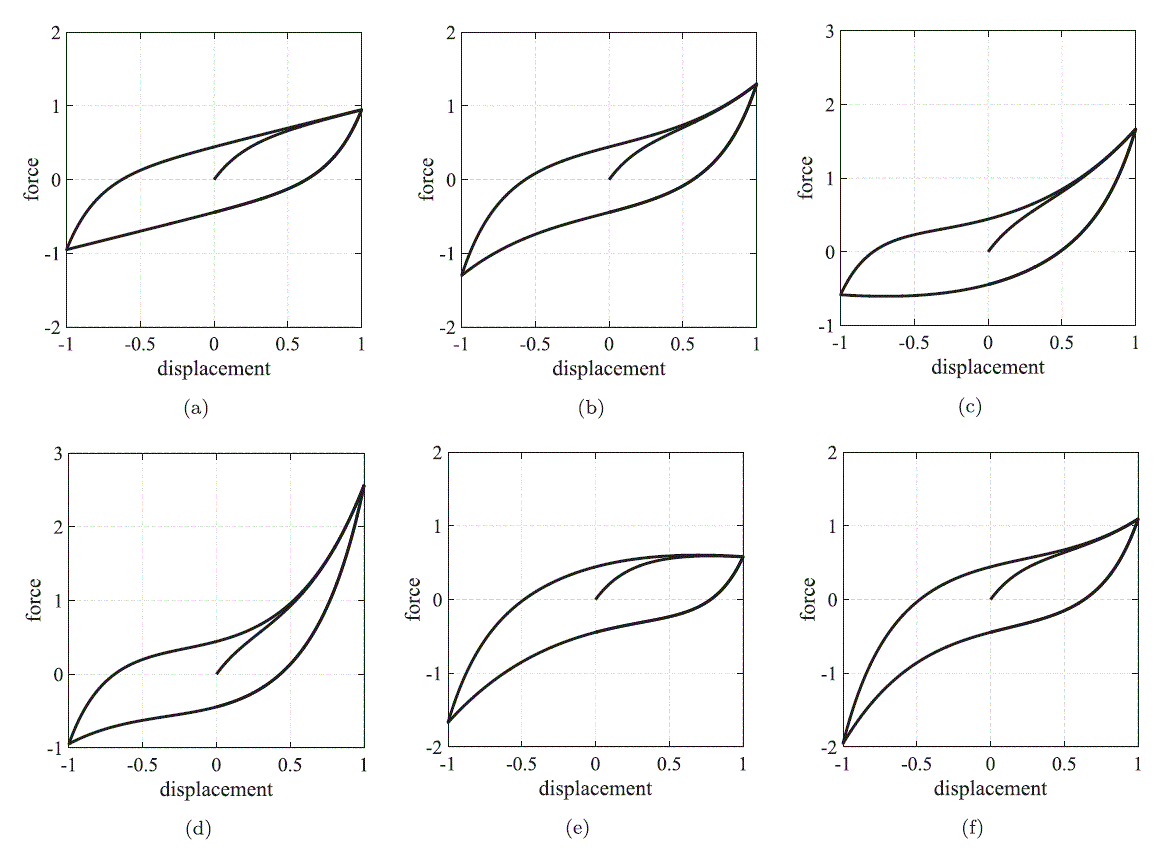
Parameters $beta1 and $beta2 rule the hardening-softening behavior as well as asymmetry. Specifically, different loop shapes can be obtained by adopting different combinations of such parameters:

Loop	obtained for:
a	\(\beta_1 = \beta_2 = 0\)
b	\(\beta_1 = \beta_2 > 0\)
c	\(\beta_1 >0; \beta_2 = 0\)
d	\(\beta_1 > \beta_2 > 0\)
e	\(\beta_1 =0; \beta_2 > 0\)
d	\(\beta_2 > \beta_1 > 0\)

Parameter $gamma introduces a further asymmetric behavior by a modulating function:

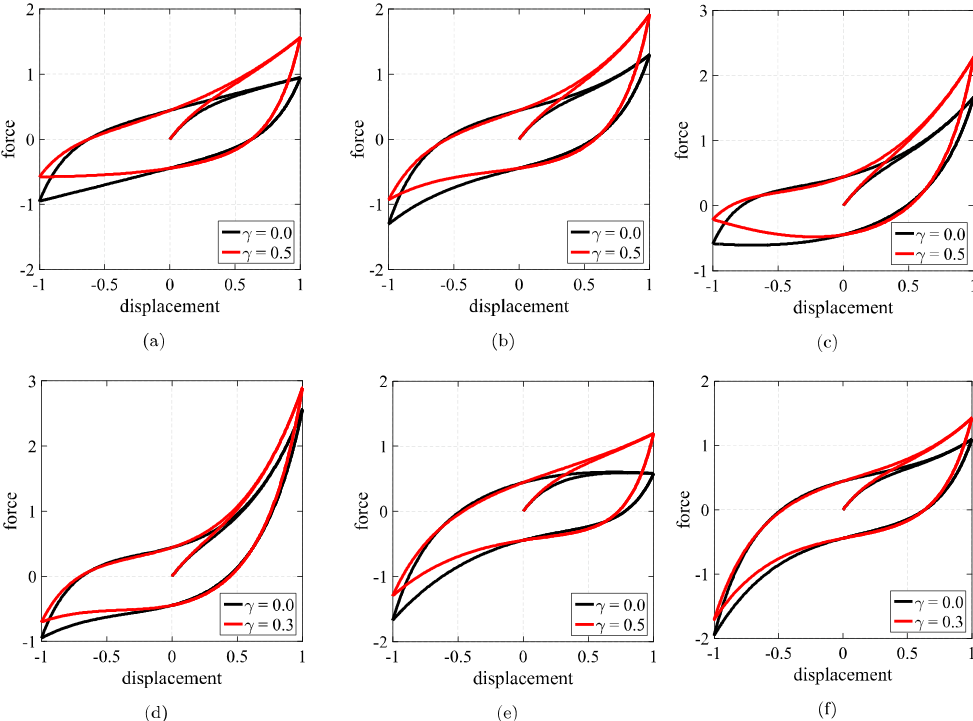
loops have been obtained by assuming $ka = 5.0, $kb = 0.5, $fo = 0.45 and:

Loop	$beta1	$beta2	$gamma
a	0.0	0.0	0.5
b	1.0	1.0	0.5
c	1.0	0.0	0.5
d	1.5	1.0	0.3
e	0.0	1.0	0.5
f	1.0	1.3	0.3

Example

The following constructs a HystereticAsym material with tag 1, parameters corresponding to line (d) of the table above.

1. Tcl Code

uniaxialMaterial HystereticAsym 1 5.0 0.5 0.45 1.5 1.0 0.3

2. Python Code

uniaxialMaterial('HystereticAsym', 1, 5.0, 0.5, 0.45, 1.5, 1.0, 0.3)

Code Developed by: Salvatore Sessa, University of Naples Federico II, Italy

[VaianaEtAl2021] (1,2)

Vaiana, N., Sessa, S. and Rosati, L. (2021). “A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena.” Mechanical Systems and Signal Processing, 146: 106984. DOI: https://doi.org/10.1016/j.ymssp.2020.106984