3.1.5.30. Jankowski Impact Material

This command is used to construct the uniaxial Jankowski Impact Material

uniaxialMaterial JankowskiImpact $matTag $Kh $xi $Meff $gap <$n>

Argument	Type	Description
$matTag	integer	integer tag identifying material.
$Kh	float	nonlinear Hertz contact stiffness.
$xi	float	impact damping ratio.
$Meff	float	effective mass.
$gap	float	initial gap
$n	float	indentation exponent (optional with default value of 1.5).

Note

This material is implemented as a compression-only gap material, so $gap should be input as a negative value.

This material model follows the constitutive law

\[\begin{split}f_c(t) = \left\{ \begin{array}{ }k_h (\delta(t)-g)^n + c_J(t) \dot{\delta}(t) & \quad \dot{\delta}(t) > 0 \\ k_h (\delta(t)-g)^n & \quad {\dot{\delta(t)} \leq 0} \end{array}\right.\end{split}\]

where t is time, $f_c (t)$ is the contact force, $k_h$ is the nonlinear Hertz contact stiffness ($Kh), $\delta(t)$ is the indentation, g is the initial gap ($gap), n is the indentation exponent ($n), and $\dot{\delta}(t)$ is the indentation velocity. Damping is only applied during the approach phase, when $\delta (t) > 0$. The damping coefficient $c_J`$ is computed as

\[c_h = 2 \xi_j \sqrt{ m_{\textrm{eff}} k_h (\delta(t) -g)^{n-1}}\]

where $m_{\textrm{eff}}$ is the effective mass of the system ($Meff), computed using the masses of the coliding bodies $m_1$ and $m_2$:

\[m_{\textrm{eff}} = \frac{m_1 m_2}{m_1 + m_2}\]

The damping ratio $\xi_j$ ($xi) is usually related to the coefficient of restitution, represented by e. The recommended form of $\xi_j$ is

\[\xi = \frac{9\sqrt{5}}{2} (\frac{1-e^2}{e(e(9\pi-16)+16)})\]

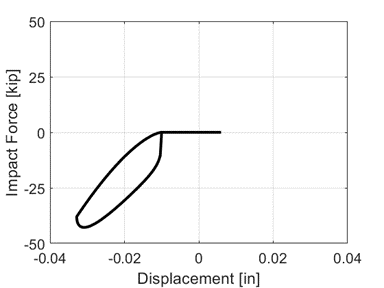
Response of the JankowskiImpact material during impact:

Note that the flat displacement from 0 to roughly minus 0.01 inch displacement is caused by the gap parameter.

Code Developed by: Patrick J. Hughes, UC San Diego

[Jankowski2005]

Non-linear viscoelastic modelling of earthquake-induced structural pounding. Earthquake Engineering and Structural Dynamics 2005; 34(6): 595–611. DOI: 10.1002/eqe.434.

[Jankowski2006]

Analytical expression between the impact damping ratio and the coefficient of restitution in the non-linear viscoelastic model of structural pounding. Earthquake Engineering and Structural Dynamics 2006; 35(4): 517–524. DOI: 10.1002/eqe.537.

[Jankowski2007]

Jankowski R. Theoretical and experimental assessment of parameters for the non-linear viscoelastic model of structural pounding. Journal of Theoretical and Applied Mechanics (Poland) 2007.

[Hughes2020]

Hughes PJ, Mosqueda G. Evaluation of uniaxial contact models for moat wall pounding simulations. Earthquake Engineering and Structural Dynamics 2020(March): 12–14. DOI: 10.1002/eqe.3285.