3.1.5.37. TzLiq1 Material

The command constructs a uniaxial t-z material that incorporates liquefaction effects. This t-z material is used with a zeroLength element to connect a pile (beam-column element) to a 2 D plane-strain FE mesh. The t-z material obtains the average mean effective stress (which decreases with increasing excess pore pressure) from two specified soil elements. Currently, the implementation requires that the specified soil elements consist of FluidSolidPorousMaterials in FourNodeQuad elements.

uniaxialMaterial TzLiq1 $matTag $soilType $tult $Z50 <$c> $ele1 $ele2

uniaxialMaterial TzLiq1 $matTag $soilType $tult $Z50 <$c> -timeSeries $tag

Argument	Type	Description
$matTag	integer	integer tag identifying material
$soilType	integer	= 1 or 2. (see notes of TzSimple1 Material)
$tult	float	Ultimate capacity of the t-z material.
$Z50	float	Displacement at which 50% of tult is mobilized in monotonic loading.
$c	float	The viscous damping term (dashpot).
$ele1 $ele2	integer	are the eleTag (element numbers) for the two solid elements from which TzLiq1 will obtain mean effective stresses and excess pore pressures.
$seriesTag	integer	alternatively mean effective stress can be supplied by a time series by specifying the text string -timeSeries and the tag of the series $seriesTag. (see Time Series Command)

To model the effects of liquefaction with TzLiq1, it is necessary to use the material stage updating command:

updateMaterialStage  –material matNum  –stage sNum

Argument	Type	Description
$matNum	integer	material number (for TzLiq1)
$sNum	integer	desired stage (valid values are 0 & 1).

Note

With sNum=0, the TzLiq1 behavior will be independent of any pore pressure in the specified solidElem’s.

When updateMaterialStage first sets sNum=1, TzLiq1 will obtain the average mean effective stress in the two solidElem’s and treat it as the initial consolidation stress prior to undrained loading. Thereafter, the behavior of TzLiq1 will depend on the mean effective stresses (and hence excess pore pressures) in the solidElem’s.

The default value of sNum is 0 (i.e., sNum=0 if updateMaterialStage is not called).

Note that the updateMaterialStage command is used with some soil material models, and that sNum=0 generally corresponds to the application of gravity loads (e.g., elastic behavior with no excess pore pressure development) and sNum=1 generally corresponds to undrained loading (e.g., plastic behavior with excess pore pressure development).

Also refer to the notes of TzSimple1 Material

TzLiq1 inherits TzSimple1 and modifies its response based on the mean effective stresses (and hence excess pore pressures) in the specified solid soil elements. The logic and implementation are the same as for how PyLiq1 Material inherits and modifies PySimple1 Material.

The constitutive response of TzLiq1 is taken as the constitutive response of TzSimple1 Material scaled in proportion to the mean effective stress within the specified solid soil elements or defined by the time series data. This means that the ultimate capacity (tult) and tangent modulus are scaled by a factor of (1-\(r_u\)). The TzLiq1 material behaves identically to the TzSimple1 material if there is no excess pore water pressure (i.e., sNum = 0 or \(r_u=0\)). The behaviour of Tzliq1 material in presense of excess pore pressure in soil is shown in Fig. 3.1.5.18. Another example illustrating the use of TzLiq1 material for modeling shaft capacity in liquefiable soils is presented in Fig. 3.1.5.20 of QzLiq1 Material.

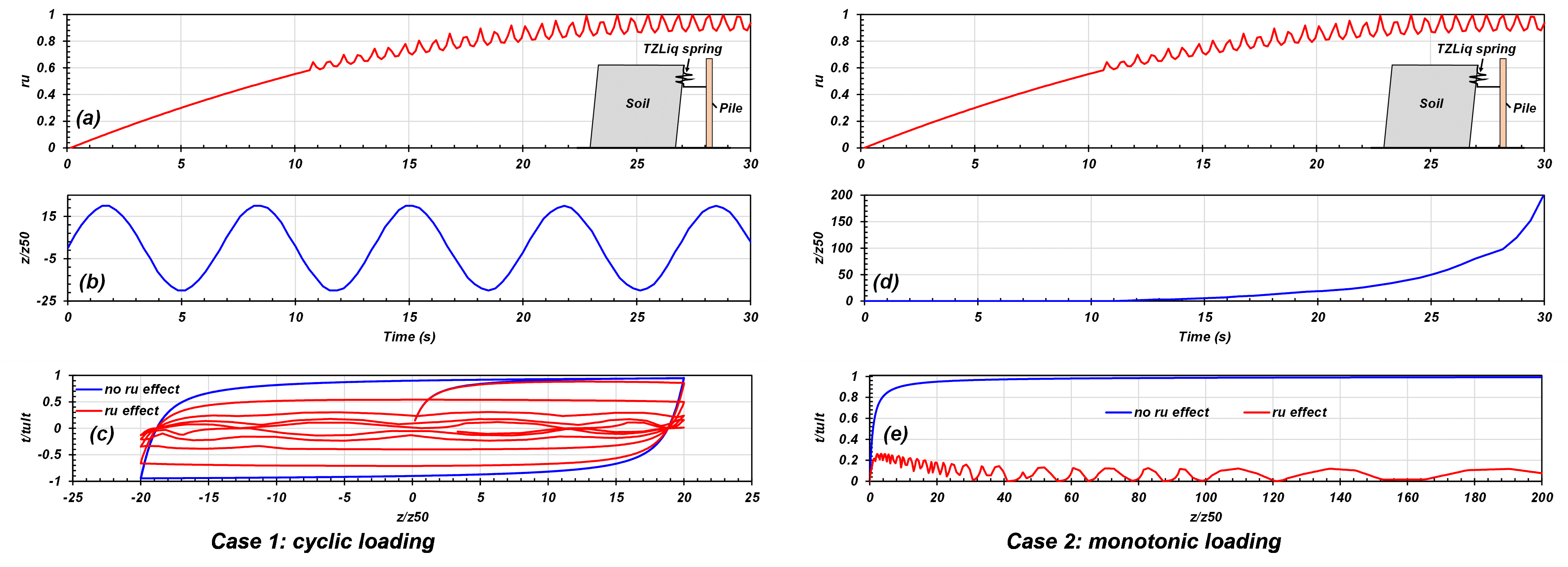
Fig. 3.1.5.18 TZLiq material response “with \(r_u\)” and “no \(r_u\)” effect during Case 1: cyclic loading and Case 2: monotonic loading.

Example 1 : TZLiq Material Response “with \(r_u\)” and “no \(r_u\)” effect during cyclic and monotonic loading | TZLiqExample_1.py TZLiqExample_2.py

Fig. 3.1.5.18 shows the material response of TZLiq1 spring in the presence of excess pore pressure in the soil. The model consisted of a movable pile node and a fixed soil node. The excess pore pressure ratio \(r_u\) calculated from the mean effective stress applied to the TZLiq spring is shown in Fig. 3.1.5.18 (a). Two separate cases (Case 1 and Case 2) were analyzed to illustrate the behavior of TZLiq spring for cyclic and monotonic loading in liquifiable soils. The displacements were applied on the pile, and the response of the TZLiq spring was recorded.

In Case 1, cyclic loading was applied to the TZLiq spring [Fig. 3.1.5.18 (b)]. The response of the TZLiq spring was recorded for two scenarios: “no \(r_u\)” and “with \(r_u\)” effect. In the first scenario, “no \(r_u\) effect”, the TZLiq spring behaved independently of excess pore presses in soil (i.e, sNum=0). As expected, the cyclic behavior of TZLiq material was similar to the TZSimple material showing no effect of excess pore pressure on the capacity and stiffness of the spring [Fig. 3.1.5.18 (c)]. In the second scenario, “with \(r_u\) effect”, the TZLiq material response was affected by the presence of excess pore pressure in the soil. To model this scenario, the sNum in the material update command was set to 1. The response is shown in Fig. 3.1.5.18 (c). As excess pore pressure (or \(r_u\)) increased in soil, the capacity and stiffness of the TZLiq spring decreased. In the first cycle, at about \(t \approx 2 sec\), with excess pore pressure ratio of \(r_u \approx 0.1\) and \(z/z_{50} \approx 20\), the ultimate capacity of the TZLiq spring decreased to about \(90 \% t_{ult}\). In the second cycle, at about \(t \approx 8.5 sec\), with increased excess pore pressure ratio of \(r_u \approx 0.5\) and \(z/z_{50} \approx 20\), the mobilized resistance of the TZLiq spring decreased to about \(50 \% t_{ult}\) which is equal to \(50 \%\) of the corresponding mobilized resistance for the case of “no \(r_u\) effect” [Fig. 3.1.5.18 (c)]. When the soil nearly liquefied \(r_u\geq0.95\), the QZLiq capacity and stiffness approached zero.

In Case 2, a monotonic loading was applied to the TZLiq spring [Fig. 3.1.5.18 (d)]. The response of the TZLiq spring was again recorded for two scenarios: “no \(r_u\)” and “with \(r_u\)” effect. In the first scenario, “no \(r_u\) effect”, the TZLiq spring behaved independently of excess pore presses in soil (i.e, sNum=0). As expected, as displacement increased the mobilized force on the TZLiq spring increased until the full capacity was mobilized (i.e., \(t/t_{ult}=1\)) [Fig. 3.1.5.18 (d)]. In the second scenario, “with \(r_u\) effect”, the TZLiq material response was affected by the excess pore pressure ratio \(r_u\) in soil. While the relative movement of the pile node always increased, the mobilized shaft resistance \(t/t_{ult}\) showed a cyclic response Fig. 3.1.5.18 (e)] because of the cyclic nature of the applied excess pore pressures [Fig. 3.1.5.18 (a)]. When the excess pore pressures increased, softening occurred, resulting in the decrease of mobilized shaft resistance. However, when excess pore pressures decreased, hardening occurred, and the mobilized shaft resistance increased.

The following constructs a TzSimple material with tag 1, soil type 2, \(t_{ult}\) of 100.0 and a \(Z_{50}\) of 1e-5. The viscous daming term c is set to be 0.0 and the mean effective stress is supplied by the timeseries tag 1.

1. Tcl Code

uniaxialMaterial TzLiq1 1  2  100.0  1e-5 0.0 -timeSeries 1

2. Python Code

uniaxialMaterial('TzLiq1', 1, 2, 100.0, 1e-5, 0.0, "-timeSeries", 1)

Code Developed by: Ross Boulanger, UC Davis

[BoulangerEtAl1999]

Boulanger, R. W., Curras, C. J., Kutter, B. L., Wilson, D. W., and Abghari, A. (1999). “Seismic soil-pile-structure interaction experiments and analyses.” Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 125(9): 750-759.