3.1.10.28. LehighJoint2D Element

This command is used to construct a LehighJoint2D element object, which is a 2D planar element with 4 nodes, each having 3 degrees of freedom (DOFs) per node.

3.1.10.28.1. Command Lines

TCL:

element LehighJoint $eleTag $iNode $jNnode $kNode $lNode $matTag1 $matTag2 $matTag3 $matTag4 $matTag5 $matTag6 $matTag7 $matTag8 $matTag9

Python:

element('LehighJoint2D', eleTag, iNode, jNode, kNode, lNode, matTag1, matTag2, matTag3, matTag4, matTag5, matTag6, matTag7, matTag8, matTag9)

where:

Argument	Type	Description
$eleTag	integer	Unique element object tag
$iNode … $lNode	integer	Node tags
$matTag1	integer	Uniaxial material tag for horizontal extension
$matTag2	integer	Uniaxial material tag for vertical extension
$matTag3	integer	Uniaxial material tag for shear distortion
$matTag4	integer	Uniaxial material tag for beam flexure
$matTag5	integer	Uniaxial material tag for column flexure
$matTag6	integer	Uniaxial material tag for asymmetric beam flexure
$matTag7	integer	Uniaxial material tag for asymmetric column flexure
$matTag8	integer	Uniaxial material tag for beam varying shear distortion
$matTag9	integer	Uniaxial material tag for column varying shear distorsion

Notes

1. The node tags shall be entered in a counter-clockwise order.

2. The uniaxial material tags represents one of the nine deformation modes present in the element depicted in the figure below.

3. The force-deformation relation in matTag3 is defined with tri-linear nonlinearity and all other force-deformation relations are modeled with linear behavior.

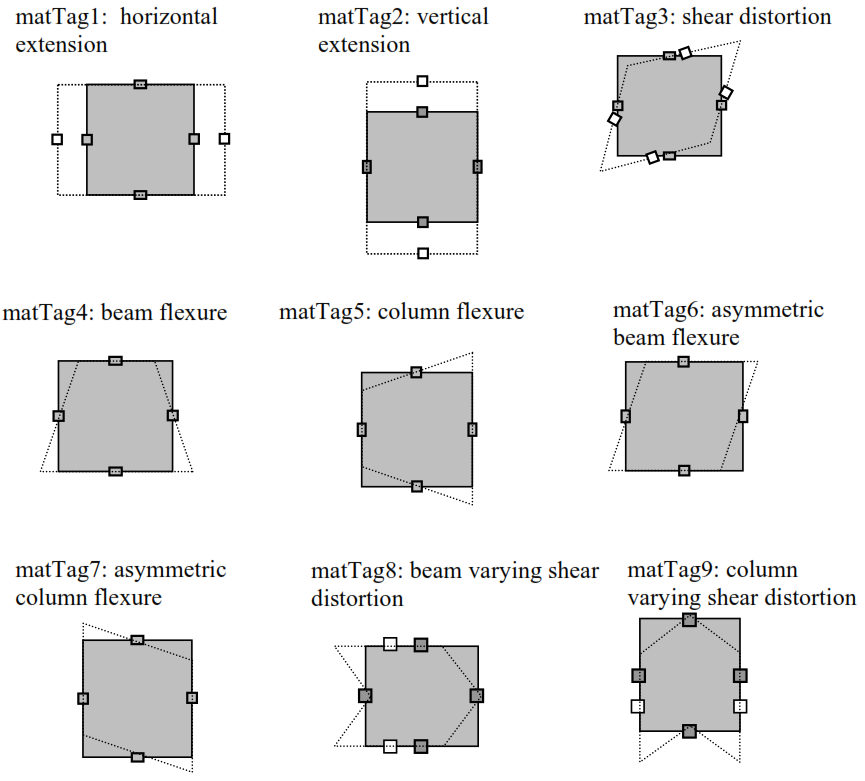
Fig. 3.1.10.29 LehighJoint2D Element: The deformation modes in the panel zone.

3.1.10.28.2. Examples

Command Lines

The following example constructs constructs a LehighJoint2D joint element with element tag 4, that is connected to nodes 2, 3, 4 and 5. The element uses uniaxial material object tags from 1001 to 1009 for the panel deformation modes.

1. Tcl

element LehighJoint 4 2 3 4 5 1001 1002 1003 1004 1005 1006 1007 1008 1009;

2. Python

element('LehighJoint2D', 4, 2, 3, 4, 5, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009)

References

More information available in the following reference:

1. Karavasilis, Theodore & Seo, Choungyeol & Ricles, James. (2008). HybridFEM: A PROGRAM FOR DYNAMIC TIME HISTORY ANALYSIS OF 2D INELASTIC FRAMED STRUCTURES AND REAL-TIME HYBRID SIMULATION HybridFEM Version 4.2.4 User’s Manual.

2. C.Y. Seo, Y.C. Lin, R. Sause & J.M. Ricles (2009). Development of analytical models for 0.6 scale self-centering MRF with beam web friction devices. In: 6th International Conference for Steel Structures in Seismic Area (STESSA), Philadelphia. CRC Press, pp. 849-854.

The article from above is part of a conference proceedings book: Mazzolani, F., Ricles, J.M., & Sause, R. (Eds.). (2009). Behaviour of Steel Structures in Seismic Areas: STESSA 2009 (1st ed.). CRC Press. https://doi.org/10.1201/9780203861592

Code developed by: CY Seo.